概率论中经典的三门悖论问题

问题描述

三门悖论（Monty Hall Problem）是概率论中的一个经典问题，源自美国电视节目《Let’s Make a Deal》。

你面前有三扇关闭的门，背后分别是一袋钱和两只山羊，钱随机放在某扇门后，概率均等。你先选择其中一扇门（例如1号门），此时门未打开，主持人（知道门后内容）会打开另一扇门（例如2号门），展示一只山羊。你可以坚持原选择（1号门）或换到剩下的未打开的门（3号门）。

问题：是换一扇门能拿到钱的概率更高，还是不换呢？

思考过程

下面是我最开始的思考过程以及看完他人讲解后的思考：

  • 一共有三扇门，主持人排除了一扇没有钱的门，剩下了两扇门，一扇门后面是钱，另一扇后面是山羊。
    • 两扇门中选一扇，那么概率应该是一样的，选到钱和山羊的概率都是$\frac{1}{2}$。

我们从直觉上会认为换门和不换门都是一样的，这并不会改变选中钱的概率，那么我们的直觉是可靠的吗，事实确实如此吗？

让我们来分析一下上面推测中的漏洞：

  1. 我们认为主持人打开一扇门后，剩下的两扇门（初始选择的门和剩下未打开的门）似乎是对称的，因此概率均等。
    • 但实际上，主持人的行为并不是随机的，他会刻意打开一扇有山羊的门，这提供了额外的信息。
  2. 我们认为初始选择一扇门和主持人打开门是两个独立事件，但实际上它们是相关的。
    • 我们的初始选择，在三扇门中选对的概率是$\frac{1}{3}$，选错的概率是$\frac{2}{3}$（这应该是对的）。我们的初始选择会对主持人开门后的结果产生影响。
    • 如果我们初次选对了，最后选择换门，那么我们将选错；但是如果我们初次选错了，最后选择换门，那就将选对（主持人会排除一扇错误的门）；
    • 如果我们初次选对了，最后不换门，那么我们将选对；但如果我们初次选错了，最后不换门，那就将选错（主持人开门不会对结果有任何影响）。
    • 通过上面的分析我们可以看到，如果我们不换门，主持人的开门对结果并不会产生影响，我们选对的概率是$\frac{1}{3}$，选错的概率是$\frac{2}{3}$。
    • 当我们换门，主持人开门则会对结果产生影响，我们初次选对时，换门会导致最终选错的概率为$\frac{1}{3}$，我们选错时换门会导致选对概率为$\frac{2}{3}$。

是不是很神奇，初始选错的概率变成了最终选对的概率，初始选对的概率竟然成了最终选错的概率。

如果觉得有点绕，我们可以把这个问题想得极端一点：

假设有100扇门，只有一扇门后有钱，其余99扇门后是山羊。你选择一扇门后，主持人打开98扇有山羊的门，剩下你的初始选择和另一扇门。此时你还会觉得换门和不换门的概率一样吗？试想一下，你需要在100扇门中选择一扇唯一有钱的门，这个概率是$\frac{1}{100}$，而主持人为你排除了98扇没有钱的门，就留了一扇（另一扇已经被你选了），此时只要我们换门，我们选对的概率将会变成$\frac{99}{100}$。

让我们用更暴力的方法来思考这个问题，把选择换门时的所有情况都枚举出来：

假设钱在门1、门2、门3后的概率均等（各1/3），下面列出所有情况：

  1. 钱在门1：你选门1，主持人随机打开门2或门3，换门失败。
  2. 钱在门2：你选门1，主持人打开门3，换门成功。
  3. 钱在门3：你选门1，主持人打开门2，换门成功。
  4. 钱在门1：你选门2，主持人打开门3，换门成功。
  5. 钱在门2：你选门2，主持人随机打开门1或门3，换门失败。
  6. 钱在门3：你选门2，主持人打开门1，换门成功。
  7. 钱在门1：你选门3，主持人打开门2，换门成功。
  8. 钱在门2：你选门3，主持人打开门1，换门成功。
  9. 钱在门3：你选门3，主持人随机打开门1或门2，换门失败。

可以看到，选择换门时一共9种情况，其中3种失败（$\frac{1}{3}$），6种成功（$\frac{2}{3}$），因此换门选对的概率会更高。

数学推导

首先我们先来复习一下概率论的一些相关知识点：

  1. 样本空间（Sample Space）是随机现象的一切可能结果组成的集合，通常记作$S$，其中的每个元素称为样本点（Sample Point）。例如扔骰子：可能的结果为“一点”至“六点”，对应的样本空间为$S={1,2,3,4,5,6}$，其中每个数字表示骰子的点数即样本点。
  2. 样本空间的子集称为事件（Event）。比如抛掷一次骰子的样本空间为$S={1,2,3,4,5,6}$，其子集$A={1,3,5}\subset S$就是一个事件，表示”抛掷一次骰子得到奇数点”。
  3. 不能同时发生的事件，称为互斥事件（Mutually Exclusive Events），可以说两个事件是互斥的，或称它们是互不相容的。
  4. 事件中的任意一个样本点出现，则称该事件发生（Occur），否则称为未发生（Not occur）。
  5. 已知某样本空间$S$，对于其中任一事件$A$，定义一个实值函数$P$（需满足非负性、规范性、可加性，这里不再展开）则称$P(A)$为事件$A$的 概率（Probability）。
  6. 基本事件（Basic event）：指仅包含一个样本点的事件，由于基本事件包含不同的样本点，因此各个基本事件互不相容。
  7. 设$A$和$B$是样本空间$S$上的两个事件，若$P(B) > 0$，则称：$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$为“给定$B$发生的条件下，$A$的概率”，简称为条件概率（Conditional Probability）。
  8. 对于样本空间$S$上的一组事件$A_1、A_2、\cdots、A_n$，若满足互斥性（Mutually exclusive）：对于任意$i\ne j，有A_i\cap A_j=\varnothing$和完备性（Exhaustive）：$\bigcup_{i=1}^{n}A_i=S$，则称这组事件为样本空间$S$的一个分割。
  9. 全概率公式：设$A_1、A_2$、$\cdots、A_n$为样本空间$S$的一个分割，且对于任意$i\in{1,2,\cdots,n}$，有$P(A_i) > 0$。则对任意事件$B$，有：$P(B)=\sum_{i=1}^{n}P(A_i)P(B|A_i)$。

下面我们就用条件概率的方法来推导一下这个悖论：

假设你初始选择1号门，定义样本空间为：$\Omega = { (D,H)|D \in {1,2,3}, H\in {2,3},H\neq C }$，其中$D$表示有钱的那扇门，$H$表示主持人开的那扇门。

当$D=1$时，$H=2$或$H=3$；当$D=2$时，$H=3$；当$D=3$时，$H=2$。

完整样本空间为：$\Omega={ (1,2),(1,3),(2,3),(3,2) }$；

钱随机放在门后：$P(D=1)=P(D=2)=P(D=3)=\frac{1}{3}$；

如果钱在1号门后即$D=1$，主持人可以打开2、3号门，则$P(H=2|D=1) = P(H=3|D=1) = \frac{1}{2}$；

如果钱在2号门后即$D = 2$，主持人只能开3号门，则$P(H=3|D=2) = 1$；

如果钱在3号门后即$D=3$，主持人只能开2号门，则$P(H=2|D=3)=1$；

因此样本空间中的每个样本点的概率为：

$P(1,2) = P(D=1) \times P(H=2|D=1) = \frac{1}{6}$

$P(1,3) = P(D=1) \times P(H=3|D=1) = \frac{1}{6}$

$P(2,3) = P(D=2)\times P(H=3|D=2) = \frac{1}{3}$

$P(3,2) = P(D=3)\times P(H=2|D=3)=\frac{1}{3}$

设$A$为初始选对事件（钱在1号门后面），设$A’$为初始选错事件（钱不在1号门后面），$B$为改变选择后选对事件，$C$为未改变选择后选对事件。

  • $P(A)=P(1,2)+P(1,3)=\frac{1}{3}$（初始选对的概率是$\frac{1}{3}$）
  • $P(A’) = P(2,3)+P(3,2) = \frac{2}{3}$（初始选错的概率是$\frac{2}{3}$）
  • $P(B|A) = \frac{P(A\cap B)}{P(A)} = 0$（在初始选对的情况下，主持人打开一扇门后，改变选择后选对的概率是0）
  • $P(C|A) = \frac{P(C\cap A)}{P(A)} =\frac{P(A)}{P(A)} = 1$（在初始选对的情况下，主持人打开一扇门后，不改变选择后选对的概率是1）
  • $P(B|A’) = \frac{P(B\cap A’)}{P(A’)} = 1$（在初始选错的情况下，主持人打开一扇门后，改变选择后选对的概率是1）
  • $P(C|A’) = 0$（在初始选错的情况下，主持人打开一扇门后，不改变选择后选对的概率是0）

则根据全概率公式可得：

$$\begin{aligned} P(B) &= P(B|A)\times P(A)+P(B|A’)\times P(A’)\ &= 0+\frac{2}{3}\times 1 = \frac{2}{3} \end{aligned}$$

$$\begin{aligned} P(C) &= P(C|A)\times P(A)+P(C|A’)\times P(A’)\ &= \frac{1}{3}+0 = \frac{1}{3} \end{aligned}$$

综上，$P(B)>P(C)$，换一扇门能拿到钱的概率会更高。

感觉整个过程不是很简洁，应该还有更简单的方法，奈何水平有限，只能写到这种程度。

程序模拟

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import matplotlib.pyplot as plt
import matplotlib
import random
def ThreeDoorsProblem(switch, loopNum):
    win = 0  # 获得钱的次数
    total = 0  # 总次数
    win_rates = []  # 记录每次实验后的获奖概率
    for i in range(loopNum):
        doors = [0, 1, 2]  # 三扇门
        prize = random.randint(0, 2)  # 随机选择一扇门作为有钱的门
        choice = random.randint(0, 2)  # 你随机选择了一扇门

        doors.remove(prize)  # 剔除有钱的门
        if choice in doors:  # 如果你没有选到有钱的门
            doors.remove(choice)  # 剔除你选择的门
        compere = random.choice(doors)  # 主持人打开一扇空门
        if switch:  # 如果你决定换门
            choice = 3 - choice - compere  # 换门
        total += 1
        if choice == prize:  # 如果你选中了有钱的门
            win += 1
        win_rates.append(win / total)  # 记录当前选中概率
    return win_rates  # 返回每次实验后的获奖概率
# 实验次数
loopNum = 1000
# 换门策略的获奖概率
switch_win_rates = ThreeDoorsProblem(True, loopNum)
# 不换门策略的获奖概率
no_switch_win_rates = ThreeDoorsProblem(False, loopNum)
# 可视化部分
matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
matplotlib.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
plt.figure(figsize=(10, 6))
plt.plot(range(loopNum), switch_win_rates, label='换门策略', color='blue')
plt.plot(range(loopNum), no_switch_win_rates, label='不换门策略', color='red')
plt.axhline(y=2/3, color='blue', linestyle='--', label='换门策略理论值 (2/3)')
plt.axhline(y=1/3, color='red', linestyle='--', label='不换门策略理论值 (1/3)')
plt.xlabel('实验次数')
plt.ylabel('选中概率')
plt.title('换门与不换门策略的选中概率随实验次数的变化')
plt.legend()
plt.grid(True)
plt.show()

执行结果：

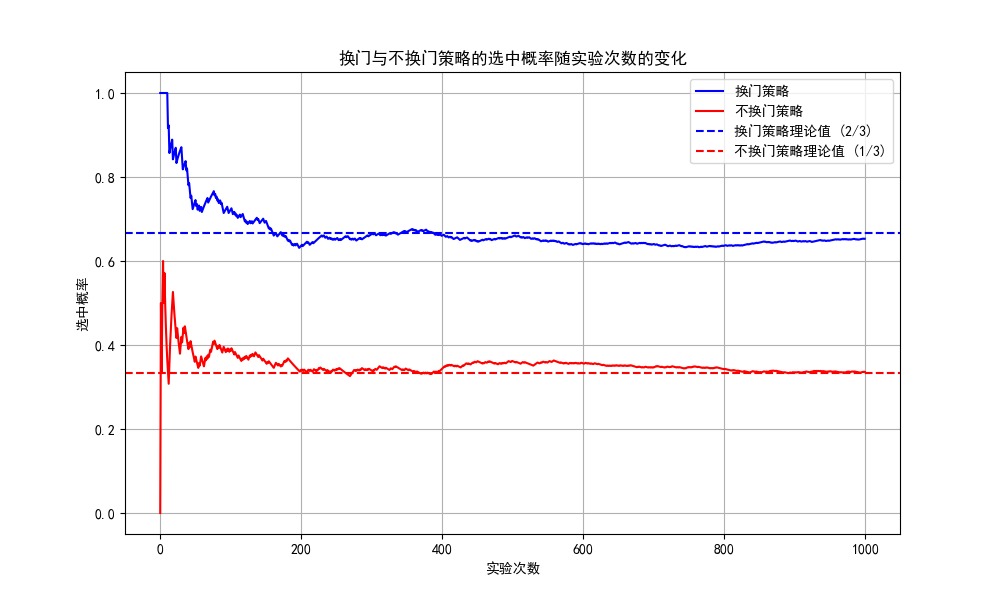
从程序模拟结果来看，随着实验次数的增加换门策略能够选中的概率确实在逐渐逼近$\frac{2}{3}$；不换门策略能够选中的概率也确实在逐渐逼近$\frac{1}{3}$，这也进一步验证了我们最初的直觉是错误的。

参考资料

[1] 【【漫士】99%的人都会答错！为什么概率这么反直觉？】 【精准空降到 02:30】

[2] 【一些反直觉的概率问题-小时百科】

[3] 【如何通俗解释条件概率】