偏导数和梯度下降

梯度下降（Gradient Descent） 最早由法国数学家奥古斯丁·路易斯·柯西（没错，就是我们在数学书上经常见到的那个柯西）在他1847年发表的论文——《Méthode générale pour la résolution des systèmes d’équations simultanées》中提出。这一方法最初是为了处理天文计算中的方程求解问题，特别是计算天体轨道的方程，上个世纪80年代，随着计算机技术和人工智能的发展，梯度下降法在机器学习领域得到广泛应用。

本期文章我们就以通俗浅显的文字来聊一聊梯度下降法。

偏导数

先来回顾一下偏导数（Partial Derivative） 的知识。

我们知道导数是函数在某一点的瞬时变化率，在几何上表示切线的斜率，而这条切线就叫做微分（Differential）。说白了导数就是一个数，也就是在某个点的斜率，而微分则是这个斜率乘以自变量的增量（$\mathrm d x$），也就是一条直线，用公式表示出来就是这样的：

$$ \underbrace{\mathrm{d}y}_{\text{微分} } = \underbrace{f’(x)}_{\text{导数} } \mathrm{d}x $$

通过下面的图像可以对导数和微分有一个更直观的感受。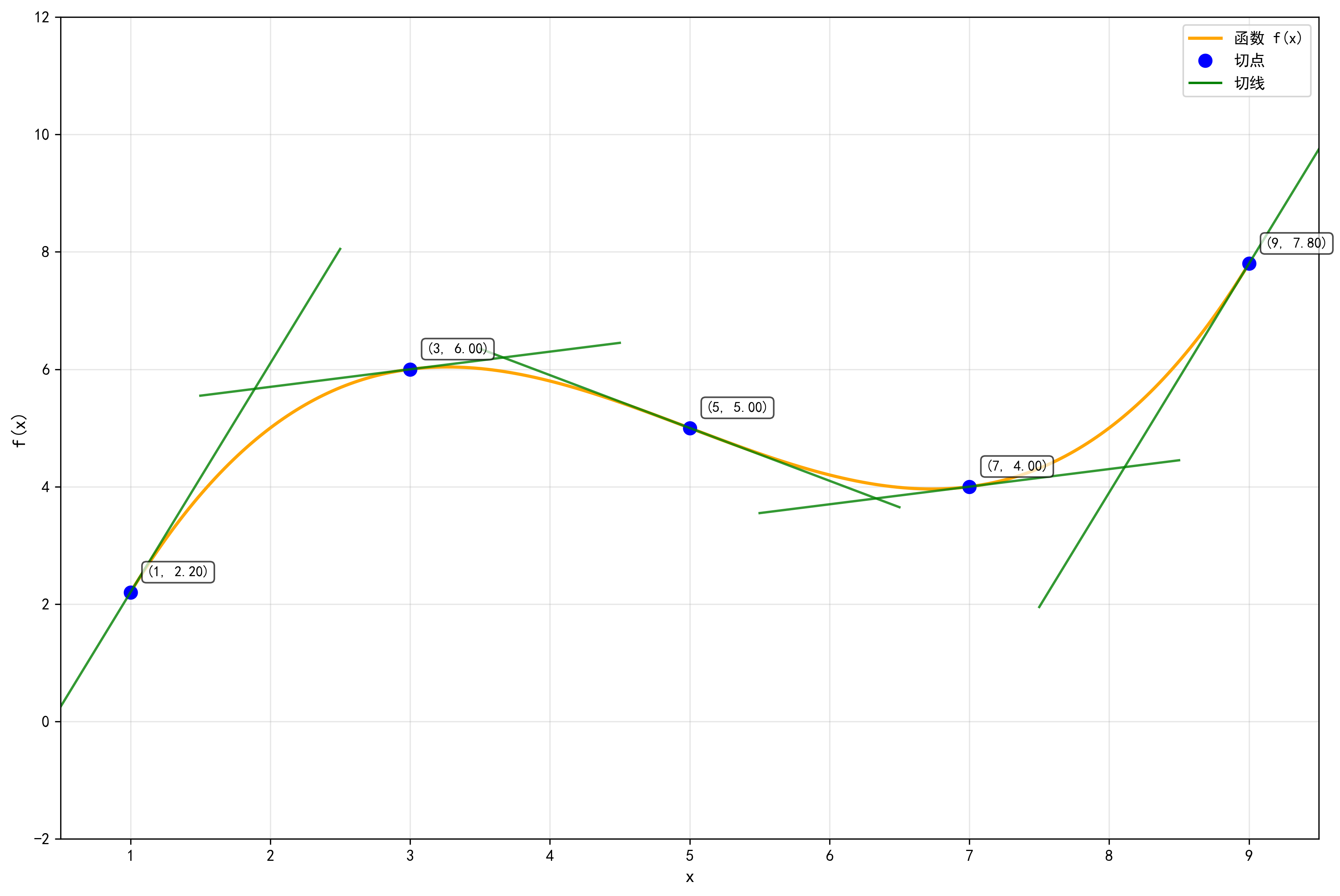

通过上面的图像可以看到，绿色的切线（微分）实际上近似了橙色的曲线，如果我们将切点取得更多、更密一些这个差距会进一步缩小。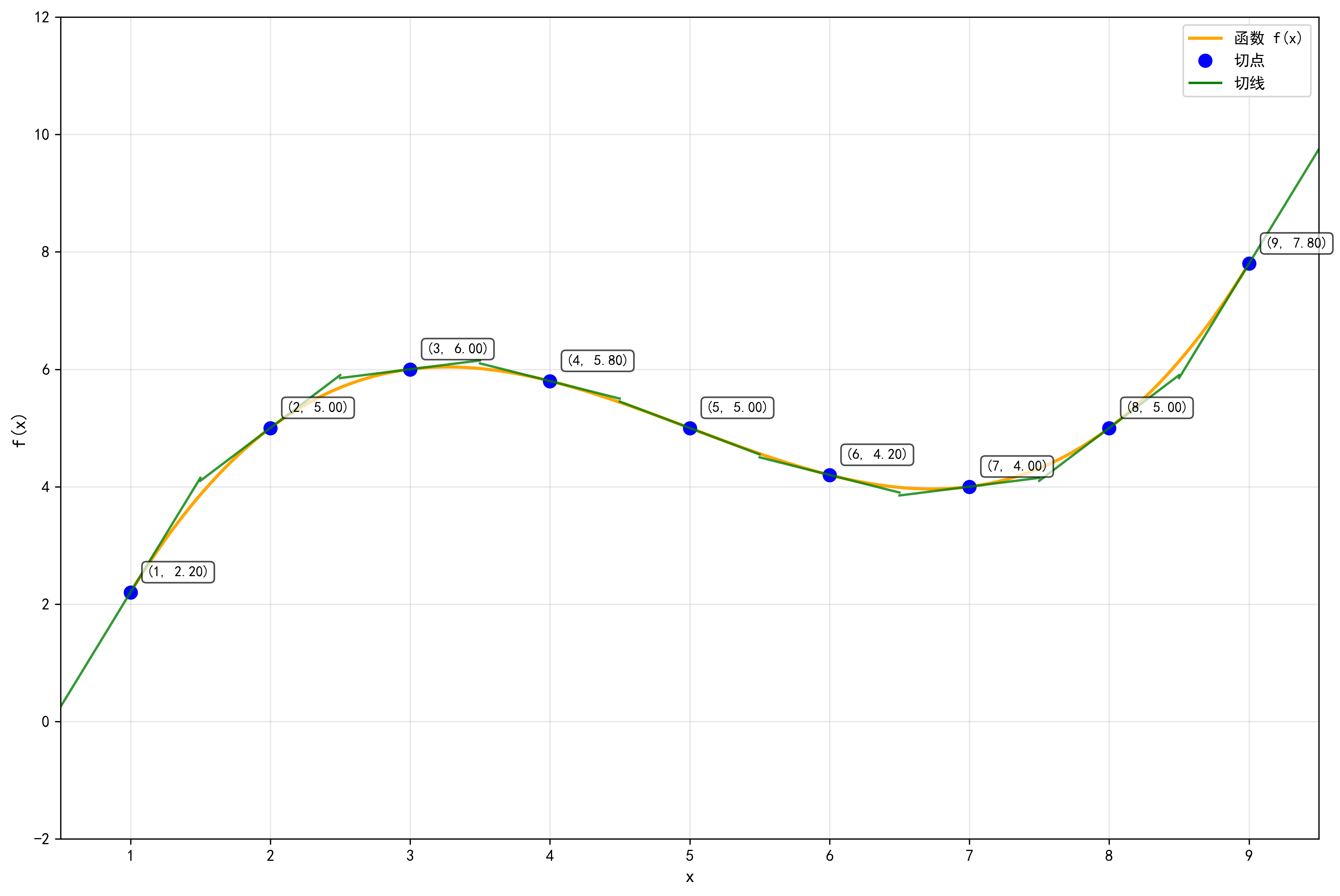

偏导数的概念与导数相差无几，导数、微分是一元函数（只有一个自变量）世界里的概念，偏导数和偏微分则是多元函数（有一个以上自变量）世界里的概念。对多元函数的某个变量求导数就称为求**偏导数(Partial Derivative)**。下面以一个3维曲面来说明。

解释下上面的图像：

  • 橙色的曲面是函数$z = f(x,y)$
  • 蓝色的曲线是函数$z = f(x=x_0,y)$
  • 绿色的曲线是函数$z = f(x,y=y_0)$
  • 灰色实线是在红色点处$(x_0,y_0,z_0)$函数对$x$的偏微分（即偏导数乘上自变量增量$\mathrm dx$）
  • 灰色虚线是在红色点处$(x_0,y_0,z_0)$函数对$y$的偏微分（即偏导数乘上自变量增量$\mathrm dy$）
    对于灰色实线，它是对绿色曲线（$z = f(x,y=y_0)$）在$(x_0,y_0,z_0)$附近的线性近似；对于灰色虚线，它是对蓝色曲线（$z = f(x=x_0,y)$）在$(x_0,y_0,z_0)$附近的线性近似。

    从图中可以看到，灰色实线的取值中$y$值是固定不变的，它是对$x$的偏微分；再看灰色虚线的取值中$x$的值是固定不变的，它是对$y$的偏微分。

    对于它们在$x=x_0,y=y_0$处的斜率（偏导数），用公式分别表示如下： $$ \begin{align} \left. \frac{\partial z}{\partial x} \right |_{\begin{aligned}x=x_0\\y=y_0\end{aligned}} = f'(x,y_0)|_{x=x_0} =\lim_{h\to 0}\frac{f(x_0+h,y_0)-f(x_0,y_0)}{h}\\ \left. \frac{\partial z}{\partial y} \right |_{\begin{aligned}x=x_0\\y=y_0\end{aligned}} = f'(x_0,y)|_{y=y_0} =\lim_{h\to 0}\frac{f(x_0,y_0+h)-f(x_0,y_0)}{h} \end{align} $$ 上面两个公式分别是函数$z=f(x,y)$在$(x_0,y_0)$处对$x$的偏导数，以及函数$z=f(x,y)$在$(x_0,y_0)$处对$y$的偏导数，两个公式成立的前提是极限分别存在。
    从这里，我们就知道了求偏导数的一个重要的原则：求偏导数时，将要求导数的目标变量以外的其他变量看作常数。对于函数$z = f(x,y)$，求$z$对$x$的偏导数时就将$y$看作常数，求$z$对$y$的偏导数时就将$x$看作常数。
    下面用平方和函数来简单操作一下：

$$
f(x,y) = x^2 + y^2
$$

求函数$f$在$x = 3,y = 4$时，关于$x$的偏导数$\frac{\partial f}{\partial x}$和关于$y$的偏导数$\frac{\partial f}{\partial y}$。

$$
\begin{equation}
\left. \frac{\partial f}{\partial x} \right| _{\begin{aligned}x=3\\y=4\end{aligned}} = 2x + 0 = 6
\end{equation}
$$

求关于$x$的偏导数，将$y$看作常数，$x^2$求导变为$2x$，常数求导变成0。

$$
\left.\frac{\partial f}{\partial y}\right|_{\begin{aligned}x=3\\y=4\end{aligned}} = 0 + 2y = 8
$$

求关于$y$的偏导数，将$x$看作常数，$y^2$求导变为$2y$，常数求导变成0。

用数值微分法估算偏导数

上期文章我们介绍了用数值微分法求导，那么现在让我继续用数值微分法来计算偏导数。

数值微分（中心差分法）函数的实现代码如下：

1
2
3
def numerical_diff(f,x):
	h = 1e-4
	return (f(x+h)-f(x-h)) / (2*h)

为了便于编程我们将$f(x,y) = x^2 + y^2$的自变量换成$x_0,x_1$，函数变成$f(x_0,x_1) = x_0^2 + x_1^2$

1
2
def func(x0,x1):
	return x0**2.0 + x1**2.0

利用数值微分（中心差分法），求$x_0 = 3, x_1 = 4$时，关于$x_0$的偏导数$\frac{\partial f}{\partial x_0}$

1
2
3
4
5
>>> def func_temp1(x0):
...     return x0**2.0 + 4.0**2.0
...
>>> numerical_diff(func_temp1,3.0)
6.00000000000378

提示：由于numerical_diff函数已经固定格式，且求偏导数时，目标变量以外的其他变量会被视为常量，因此我们将x0**2.0 + x1**2.0改成了x0**2.0 + 4.0**2.0

求$x_0 = 3, x_1 = 4$时，关于$x_1$的偏导数$\frac{\partial f}{\partial x_1}$

1
2
3
4
5
>>> def func_temp2(x1):
...     return 3.0**2.0 + x1**2.0
...
>>> numerical_diff(func_temp2,4.0)
7.999999999999119

同样，我们将x0**2.0 + x1**2.0改成了3.0**2.0 + x1**2.0

可以看到利用数值微分法估算得到的偏导数，与真实偏导数非常接近，误差可以忽略不计。

梯度

复习完偏导数，我们可以引入梯度（Gradient） 这个话题了。

梯度其实就是将函数关于所有自变量的偏导数放在一起组成的一个向量，以上面的$f(x_0,x_1)$函数为例，它的梯度就是$\nabla f = (\frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1})$，梯度的每个分量是函数在对应变量方向上的偏导数。

梯度是向量，有方向和大小，而导数在单变量函数中等同于梯度的大小，因此多变量情况下梯度才有方向的概念，在一元函数中讨论梯度意义不大。

梯度有一个非常重要的特性：梯度向量指向函数增长最快的方向，而它的模长是增长速率。
这样的话，梯度下降法就是沿着负梯度方向找最小值。

许多对梯度的解释都会用到“上山”、“下山”的比喻：爬山的时候，如果你想最快上山，就沿着最陡的方向走，那就是梯度的方向。相反，如果想最快下山，就沿着负梯度方向。梯度的大小就是那个方向的陡峭程度。

可以说梯度就是 “函数值变化的最强指南针” 。

梯度凭什么下降

为什么朝着梯度的方向就是最快“上山”的方向呢，为什么朝着负梯度的方向就是最快“下山”的方向呢？

为了解答这个问题，我们需要引入一个新的概念——方向导数 ：

假设有一个多元函数$f(x, y)$，在点$(x_0, y_0)$处，现在要向某个方向$\mathbf{u} = (a, b)$（单位向量）移动一小步。此时函数的变化速率称为方向导数，计算公式为：

$$
D_{\mathbf{u}} f = \underbrace{\nabla f}_{\text{梯度}} \cdot \underbrace{\mathbf{u}}_{\text{单位向量}} = \frac{\partial f}{\partial x} a + \frac{\partial f}{\partial y} b
$$

它表示函数沿向量$\mathbf{u}$方向的瞬时变化率。

更进一步，方向导数$D_{\mathbf{u}} f$其实就是梯度$\nabla f$和方向向量$\mathbf{u}$的点积：

$$
\nabla f \cdot \mathbf{u} = |\nabla f| \cdot |\mathbf{u}| \cdot \cos\theta = |\nabla f| \cdot \cos\theta
$$

解释一下：方向导数公式已经说过$\mathbf{u}$是一个单位向量，因此它长度$|\mathbf{u}|=1$；$\theta$ 则是梯度$\nabla f$和方向向量$\mathbf u$的夹角。

由于$\cos \theta \in [ -1,1]$，因此当且仅当$\cos \theta = 1 \rightarrow \theta =0$时也就是 $\mathbf{u}$ 与$\nabla f$ 同方向时方向导数达到最大值：
$$
D_{\mathbf{u}} f_{\text{max}} = |\nabla f|
$$
这样我们就说明了梯度方向$\nabla f$是方向导数最大的方向，即函数在该方向变化最快；反方向$\nabla f$则是下降最快的方向。

数值微分法计算梯度

为了更方便计算梯度，我们需要修改上面计算偏导数用到的数值微分函数（中心差分法）的实现代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def numerical_gradient(f,x):
	h = 1e-4
	grad = np.zeros_like(x) #生成与x形状相同的0向量
	for idx in range(x.size):
		temp_val = x[idx]
		x[idx] = temp_val + h
		fxh1 = f(x)
		
		x[idx] = temp_val - h
		fxh2 = f(x)
		
		grad[idx] = (fxh1 - fxh2) / (2*h)
		x[idx] = temp_val
	return grad

这里的代码看上去有些复杂其实就是从上面的分别求单个变量的偏导数改成了一次性求所有变量的偏导数，np.zeros_like(x)生成一个形状和x相同，所有元素都为0的数组，用该数组（grad）存储各个自变量的偏导数。

numerical_gradient(f, x)中，参数f为求偏导的函数，x为NumPy数组，是求偏导处自变量的取值，该函数对NumPy数组x的各个元素求近似偏导数。

现在让我们来尝试一下对$f(x_0,x_1) = x_0^2 + x_1^2$这个函数求梯度。

函数$f(x_0,x_1) = x_0^2 + x_1^2$的实现代码如下：

1
2
def func(x0,x1):
	return x0**2.0 + x1**2.0

在$(3,4)$，$(0,2)$，$(3,0)$处分别求梯度

1
2
3
4
5
6
>>> numerical_gradient(func,np.array([3.0,4.0]))
array([6., 8.])
>>> numerical_gradient(func,np.array([0.0,2.0]))
array([0., 4.])
>>> numerical_gradient(func,np.array([3.0,0.0]))
array([6., 0.])

这样我们计算出函数在$(3,4)$，$(0,2)$，$(3,0)$处的梯度分别为$(6,8)$，$(0,4)$，$(6,0)$。

如果我们分别在$x_0$和$x_1$方向上按$0.25$的间距取值，从-2取到2，然后分别求出函数在这些点的梯度，将这些梯度向量在二维平面上画出来，就可以得到下面图像：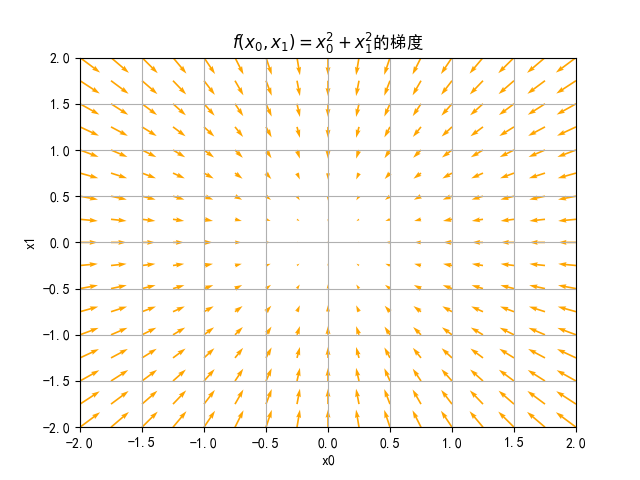

说明一下：这里所有梯度都乘了一个-1，变成负梯度向量。负梯度向量箭头的方向由$(x_0,x_1)$指向$(x_0-\frac{\partial f}{\partial x_0},x_1-\frac{\partial f}{\partial x_1})$。负梯度指示的方向是各点处的函数值减小最多的方向。

可以看到，所有梯度向量都指向了点$(0,0)$处，而这个点恰恰是函数的最小值。提示一下，这里我们只是取了一个简单的函数，恰巧所有梯度向量都指向了最小值，但现实情况中更多复杂的函数的梯度指向基本上都不是函数最小值处。

梯度下降GD

在机器学习和深度学习中经常会用到梯度下降法（Gradient Descent Method） 来训练模型，用梯度下降法 优化模型时，会计算损失函数（可将损失函数看作一个打分器，模型训练得好不好就要问它）的梯度，沿着负梯度方向调整参数（相当于“最快下山”），逐步逼近最小值（或者尽可能小的值）。

虽然负梯度的方向并不一定指向最小值，但沿着它的方向能够最大限度地减小函数的值。

在梯度下降中，函数的取值从当前位置沿着负梯度方向前进一定距离，然后在新的地方重新求梯度，再沿着新的负梯度方向前进，如此反复，不断地沿负梯度方向前进。像这样，通过不断地求梯度，逐渐减小函数值的过程就是梯度下降。梯度下降法是解决机器学习中最优化问题的常用方法，特别是在神经网络的学习中经常被使用。

寻找最小值的梯度法称为 梯度下降法(Gradient Descent Method) ，寻找最大值的梯度法称为**梯度上升法(Gradient Ascent Method)**，“上升”和“下降”仅仅是梯度正负号的区别，其求解方法是相同的。在梯度下降法中我们使用负梯度方向来更新参数，下面不再对梯度和负梯度进行区分。

对于仅有两个自变量的函数，梯度下降法用数学符号表示如下：
$$
\begin{align}
x_0’ = x_0-\eta \frac{\partial f}{\partial x_0}\
x_1’ = x_1-\eta \frac{\partial f}{\partial x_1}
\end{align}
$$
上式中，$\eta$表示下山时一步迈多远，在神经网络的学习中，称为 学习率(Learning Rate) 。学习率决定在一次学习中，应该学习多少，及在多大程度上更新参数。学习率需要先初始化为某个值，一般而言这个值过大或过小都无法抵达一个“好位置”。

上式代表一次更新，这个步骤会反复执行，逐渐减小损失函数值。这个式子只展示了两个变量的更新过程，推广到n个变量也是一样的。

结合前面的代码，下面来实现梯度下降：

1
2
3
4
5
6
def gradient_descent(f, init_x, lr=0.01, step_num=100):
	x = init_x
	for i in range(step_num):
		grad = numerical_gradient(f,x)
		x -= lr * grad
	return x

参数f是要进行梯度下降的函数，init_x是初始值，lr是学习率，step_num是梯度下降的迭代次数。numerical_gradient(f,x)会求函数的梯度，用该梯度乘以学习率得到的值进行更新操作（也就是用原来的值减去梯度乘以学习率）。

同样以函数$f(x_0,x_1)=x_0^2+x_1^2$为例，用梯度下降法求它的最小值。

1
2
3
4
5
6
>>> def func(x):
...     return x[0]**2 + x[1]**2
...
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(func, init_x, lr=0.1, step_num=100)
array([-6.11110793e-10,  8.14814391e-10])

设初始值为(-3.0, 4.0)，开始使用梯度法寻找最小值。最终的结果是(-6.1e-10, 8.1e-10)，非常接近最小值。将这个过程可视化出来就是这样的：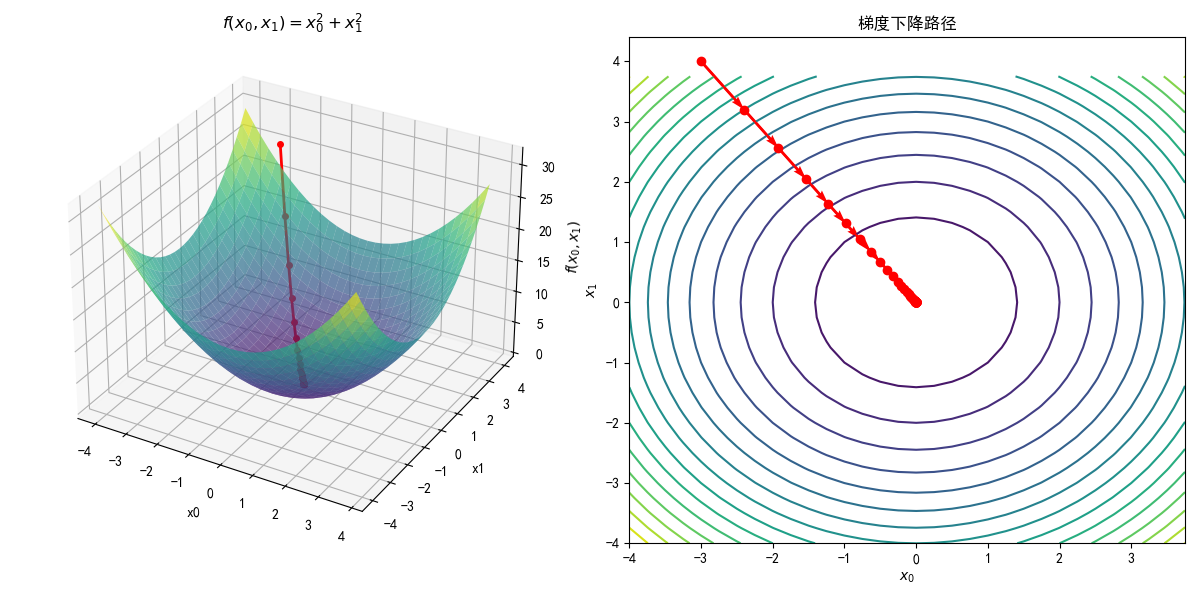

如果我们改变学习率lr的取值会怎么样呢？

当lr=0.005时，最终到达的位置为(-1.09809702, 1.46412937)，离最小值还差的远，虽然通过增加迭代次数也能够到达最小值附近，但效率太低了。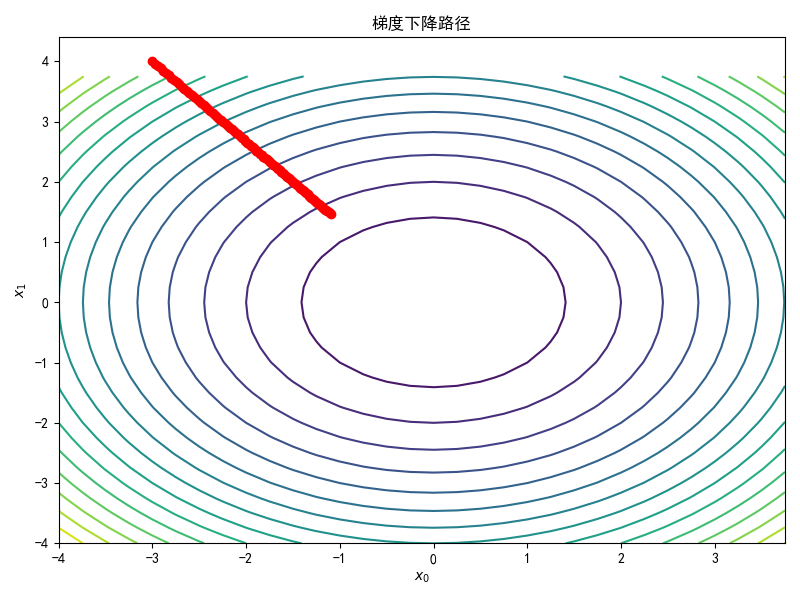

当lr=10时结果发散了

1
2
>>> gradient_descent(func, init_x, lr=10.0, step_num=100)
array([ 2.80292473e+12, -2.76020044e+12])

这表明：学习率过大会导致结果发散成一个非常大的值，学习率过小会导致参数得不到有效更新，无法逼近最小值。因此设定一个合适的学习率也非常重要，至于如何设置合适的学习率我们会在其他文章中说到。

梯度下降的局限性

有人可能会问，这函数我不一眼就看出来最小值了吗，看不出来我动手算也是能算出来的呀，哪怕我不会算我问AI也能找最小值的嘛。那么问题来了，如果这个函数有几万、几十亿参数怎么去算，现代深度学习模型莫说手算，就是用刚刚的方法去算也是不可行的。

原因之一就是上期文章提到的数值微分法的局限性：数值微分法计算效率太低了，对于每一个参数都需要多次前向计算，参数量一多，计算量急剧增加，这种情况下不能用数值微分法。对于这个问题，通常解决办法是采用反向传播(Backward Propagation) 算法。

还有的问题就是梯度下降固有的局限性。

局部最小值陷阱

梯度下降的目标就是找到梯度为0的点，函数的极小值、最小值以及被称为鞍点(Saddle Point) 的地方，梯度为0。极小值是局部最小值，也就是限定在某个范围内的最小值。鞍点是从某个方向上看是极大值，从另一个方向上看则是极小值的点。虽然梯度法是要寻找梯度为0的地方，但是那个地方不一定就是最小值（也有可能是极小值或者鞍点）​。

当函数很复杂且呈扁平状时，梯度下降可能会进入一个（几乎）平坦的地区，陷入在机器学习领域里被称为“学习高原”的无法前进的停滞期。

其他局限性和改进方法

  1. 对学习率非常敏感：学习率过大导致震荡不收敛，过小则收敛缓慢。在陡峭区域需要小学习率，在平坦区域需要大学习率，但固定学习率无法自适应。
  2. 对特征尺度敏感：若输入特征尺度（输入变量的取值范围或量纲差异）差异大（如一个特征范围是 [0,1]，另一个是 [0,1000]），梯度下降会沿大尺度特征方向震荡。
  3. 内存和效率：全批量梯度下降（Batch GD）需计算所有样本的梯度，内存和计算成本高，不适合大数据集。

基于梯度下降法和其本身具有的缺陷，又衍生出其他改进方法：

  1. 随机梯度下降（SGD）与小批量梯度下降（Mini-batch GD）：每次随机选一个样本或一小批样本计算梯度。
  2. 动量法（Momentum）：引入动量项，累积历史梯度方向，加速收敛并减少震荡。
  3. 自适应学习率方法：根据参数的历史梯度动态调整学习率。如Adam和RMSProp算法。
  4. 二阶优化方法：利用损失函数的二阶导数信息，加速收敛。如牛顿法和拟牛顿法。
  5. 启发式算法：增强全局搜索能力，避免陷入局部极小值。如遗传算法(GA) 和 粒子群优化(PSO) 。

    梯度下降过程动画

    为了更加直观地观察梯度下降的过程，我将函数$f(x_0,x_1)=x_0^2+x_1^2$，初始位置$(-3,4)$的梯度下降过程用动画画了出来。

这里只迭代了15次，所以动画最后的位置离最小值$(0,0)$还有些距离，但随着迭代次数增加这个值越来越接近最小值。

参考资料：

[1] 斋藤康毅. 深度学习入门：基于Python的理论与实现[M]. 陆宇杰, 译. 北京: 人民邮电出版社, 2018.

[2] Stuart Russell, Peter Norvig. 人工智能：现代方法[M]. 第4版. 北京: 清华大学出版社, 2020.

[3] 小时百科. 偏导数[EB/OL].

[4] 小时百科. 梯度下降[EB/OL].

[5] 维基百科. 偏导数[EB/OL].

[6] 维基百科. 梯度下降法[EB/OL].

[7] Claude Lemaréchal. Cauchy and the Gradient Method[J]. Documenta Mathematica, 2012: 251-254.